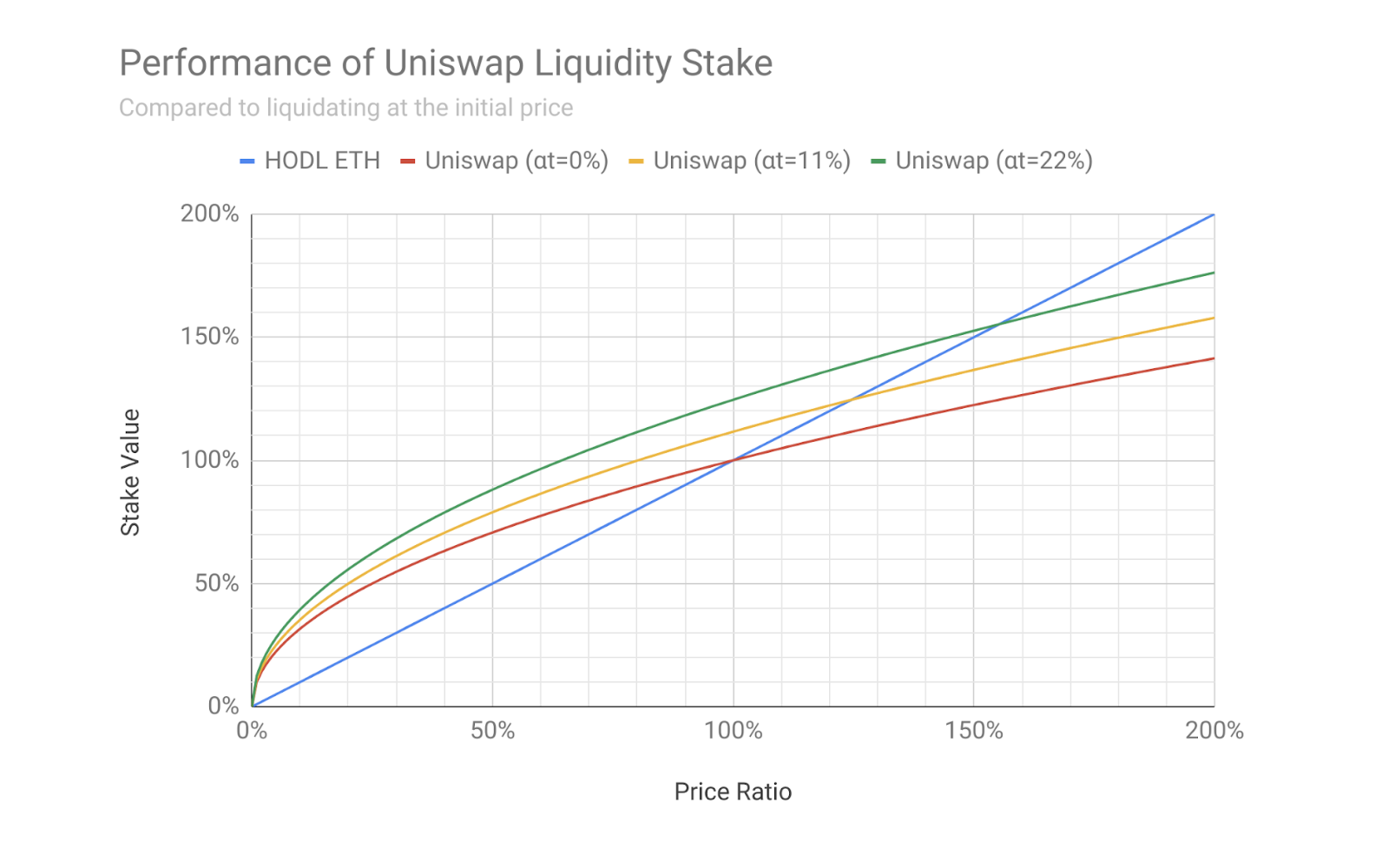
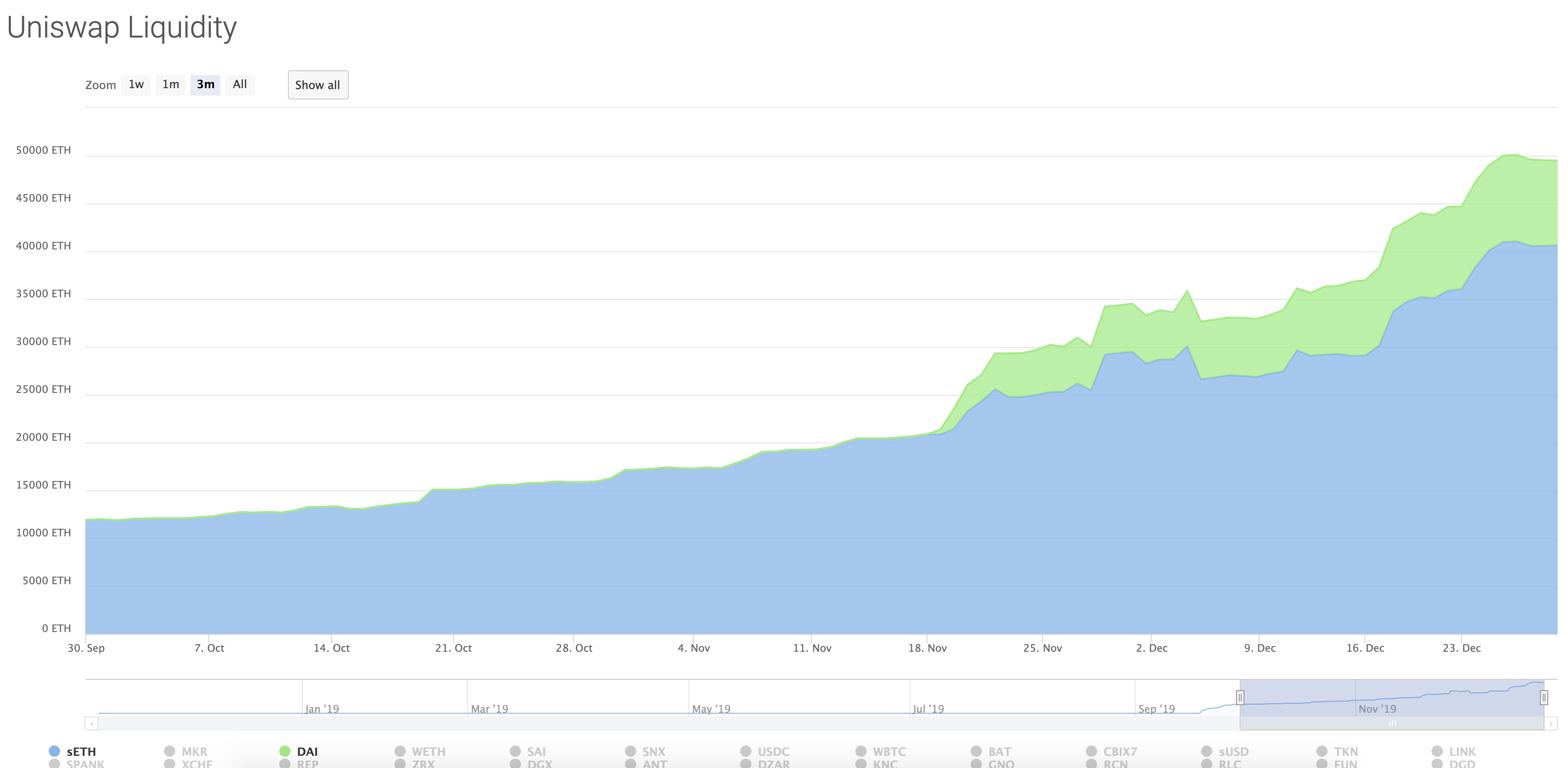
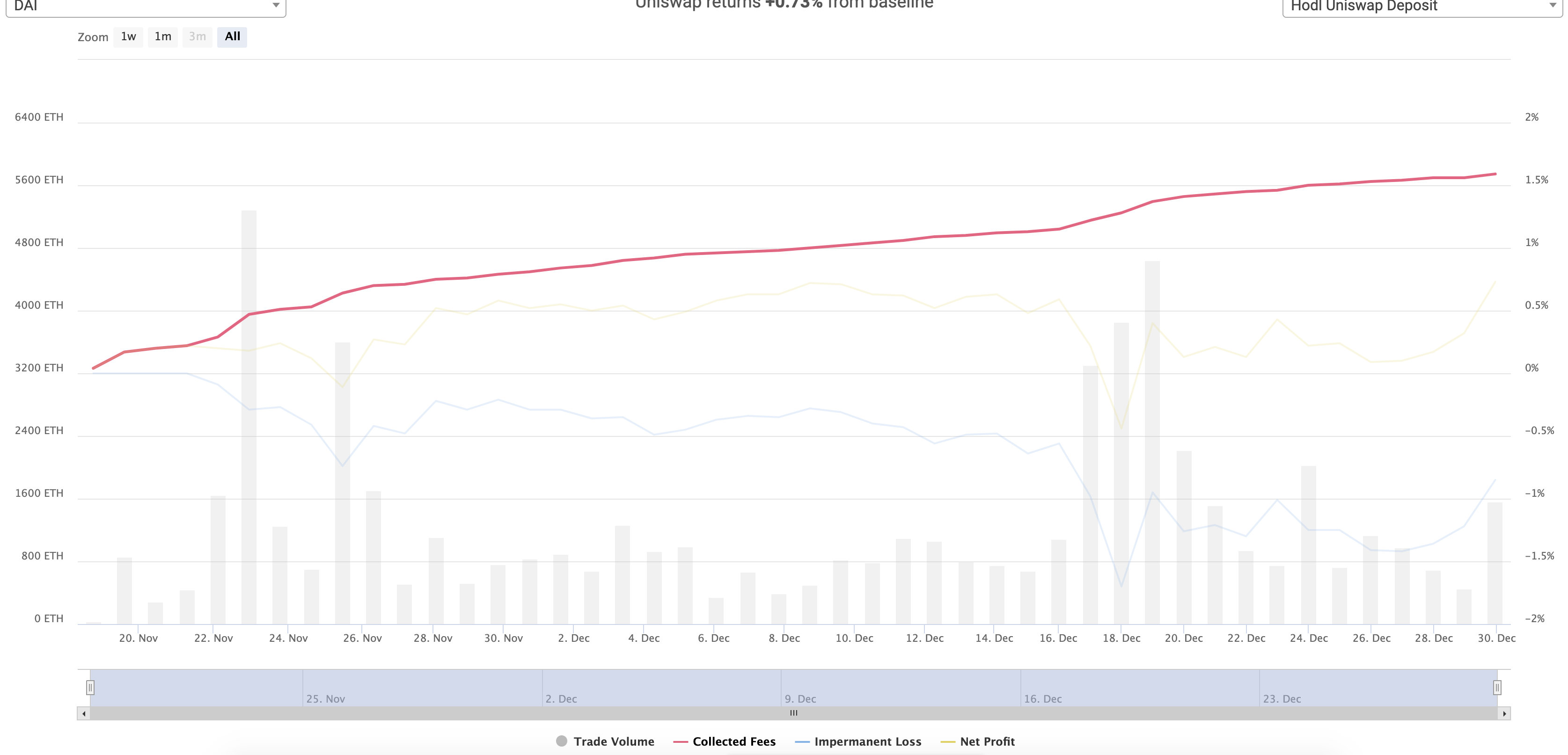
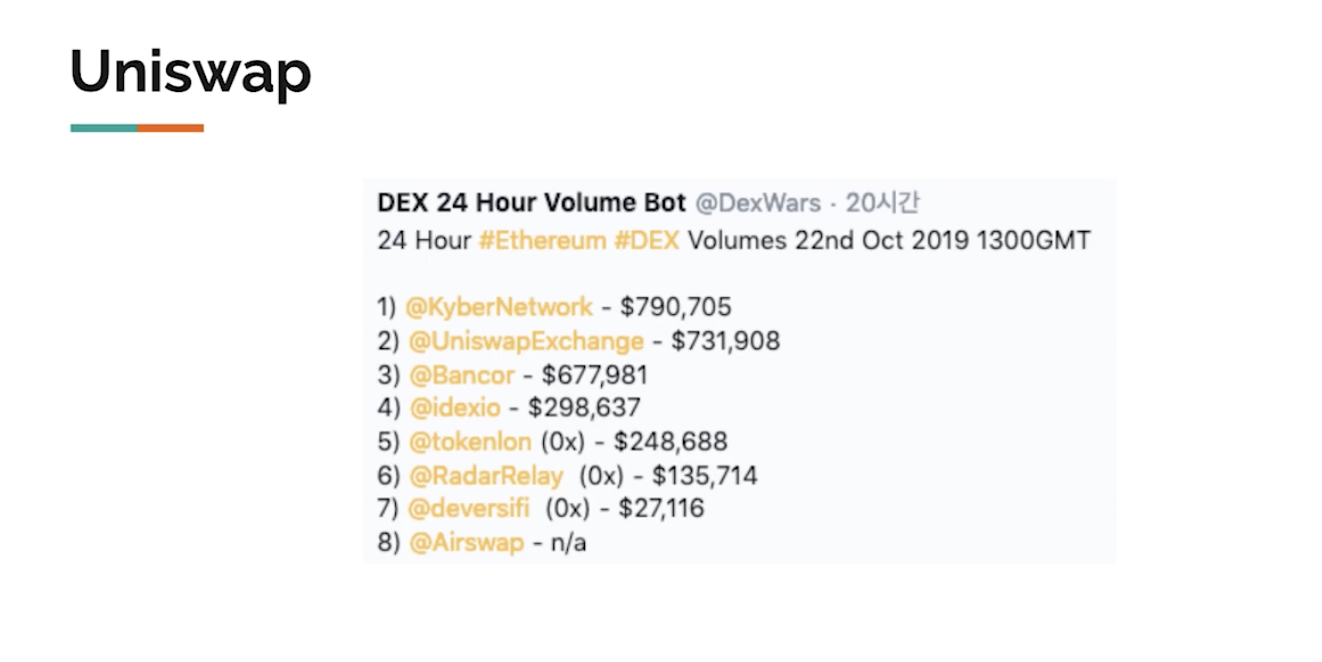
나온지 얼마 안된 핫한 책이다.
노벨상탄 경제학자들의 이론을 바탕으로 부에 대해 이야기해준다. 재밌다.
이 책을 읽고 내가 할 수 있는 건 뭘까?
- 종잣돈 모으기
- 가족에게 이 책 추천하기
- 실력 키우기
- 좋은 서비스 밴치마킹해서 괜찮은 서비스 여러 개 만들기
(독점. 과점. 진입장벽이 있는 것.)
부동산이 왜 오르는지에 대한 이사람 이야기는 재미있었다.
화폐가 생성되는 원리도 알 수 있어서 좋았다.
국가 정책에 대해서도 이해가 갔다.
읽다가 체크한것들을 적어본다.
진입장벽
상가는 넘친다. 진입장벽이 없다.
아파트는 청약통장, 진입장벽이 있다.
돈있다고 누구나 분양받는게 아니다.
수요에 비해 공급이 부족하다.
그러니 값이 오른다.
불쾌감, 불명예가 수익을 준다.
도박관련 주식
독점
돈을 벌고 싶으면 독점기업에 투자하라.
부동산은 하나의 독점기업이다.
독점 기업. 공인인증서.
남과 다른 해석
같은정보를 보고 다른 해석
거북이는 토끼에게 달리기를 하자고 하면 안된다.
수영대회를 하자고 해야한다.
자산가치, 인플레이션
부동산은 실물자산, 화폐는 가짜
화폐는 정부에서 찍어낸다. 계속 늘어난다.
정책에 따라 바뀐다.
빚을 내서 실물자산 부동산을 산다면?
빚은 시간이갈수록 빚의 가치가 떨어진다.
화폐가치는 떨어지고 실물자산 부동산 가격은 오른다.
우샹항은 맞는데, 하강과 상승 사이클을 그리면서 우상향라고 한다.
상투를 잡으면 수익 실현에 오래걸릴 수 있다.
보험업
바로 화폐를 받아서, 후일 실제가치가 떨어진 화폐로 지불을 약속하는 비즈니스
돈을 벌 수 밖에 없다.
서울이 비싼이유
우리나라 최고의 도시
교육, 즐길것, 데이트, 모든게 갖춰짐.
잘사는 사람들이 사는 곳 근처에 사라.
판교가 오른이유.
IT회사가 다 거기로 갔다.
인재가 모였다.
서울대입구가 뜬다. ㅋㅋ
이 책을 읽고 내가 땅이나 아파트를 살 수 있다면 서울대입구 근처를 알아볼것이다.
땅으로 치면, 서울대입구 근처가 앞으로 뜰 지역으로 보인다.
강남이 지금까지 대세였다면, 서울대입구는 떠오르는 태양이다.
놀거리, 먹을거리가 가득하고, 사람도 많다. 젊은 사람도 많다. 데이트하기 좋다.
요즘은 샤로수길이라고 서울대입구 앞에 생긴 거리이다.
거기다가 최고의 학교 서울대학교가 있다. 과외도 받기 쉽다.
음식, 교육, 놀거리 하나하나 갖춰지고 있는 곳이다.
강남은 계속 비쌀것 같다. 더 오를거고. 우샹항이다.
최고의 암호화폐 지갑 추천
이 내용이 도움이됐나요? 최고의 암호화폐 지갑을 추천합니다.저를 추천인으로 해주세요.
궁금한게 있으시면 언제든 댓글 달아주세요.
감사합니다.
https://jacobyu.net/categories/암호화폐/크립토닷컴/
This page is synchronized from the post: ‘[독서일기] 부의 인문학, 서울대입구가 뜰 것 같다.’